函數關係
| 時域訊號 | 角頻率表示的 傅立葉轉換 | 弧頻率表示的 傅立葉轉換 | 註釋 | |
|---|---|---|---|---|
 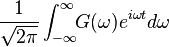 | 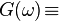  | 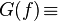 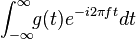 | ||
| 1 |  | 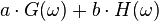 | 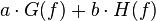 | 線性 |
| 2 | 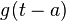 |  |  | 時域平移 |
| 3 | 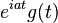 | 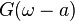 |  | 頻域平移, 轉換2的頻域對應 |
| 4 |  |  |  | 如果 值較大,則 值較大,則 會收縮到原點附近,而 會收縮到原點附近,而 會擴散並變得扁平. 當 | a |趨向無窮時,成為 Delta函數。 會擴散並變得扁平. 當 | a |趨向無窮時,成為 Delta函數。 |
| 5 |  |  |  | 傅立葉轉換的二元性性質。通過交換時域變數 和頻域變數 和頻域變數  得到. 得到. |
| 6 |  |  |  | 傅立葉轉換的微分性質 |
| 7 |  |  | 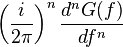 | 轉換6的頻域對應 |
| 8 | 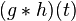 |  | 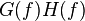 |  表示 表示  和 和  的摺積 — 這就是摺積定理 的摺積 — 這就是摺積定理 |
| 9 |  |  |  | 轉換8的頻域對應。 |
[編輯]平方可積函數
| 時域訊號 | 角頻率表示的 傅立葉轉換 | 弧頻率表示的 傅立葉轉換 | 註釋 | |
|---|---|---|---|---|
 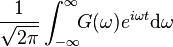 | 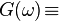 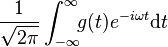 | 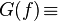  | ||
| 10 |  | 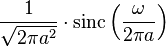 |  | 矩形脈衝和歸一化的sinc函數 |
| 11 | 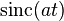 |  | 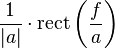 | 轉換10的頻域對應。矩形函數是理想的低通濾波器,sinc函數是這類濾波器對反因果衝擊的響應。 |
| 12 |  | 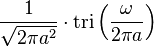 | 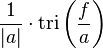 | tri 是三角形函數 |
| 13 | 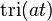 | 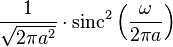 | 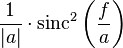 | 轉換12的頻域對應 |
| 14 | 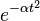 |  |  | 高斯函數 exp( − αt2) 的傅立葉轉換是他本身. 只有當 Re(α) > 0時,這是可積的。 |
| 15 | 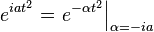 | 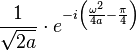 | 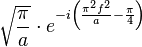 | 光學領域應用較多 |
| 16 | 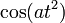 |  | 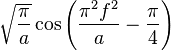 | |
| 17 |  |  |  | |
| 18 |  |  |  | a>0 |
| 19 |  |  | 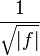 | 轉換本身就是一個公式 |
| 20 | 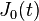 |  |  | J0(t) 是0階第一類貝索函數。 |
| 21 | 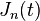 | 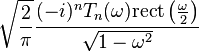 | 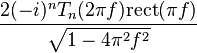 | 上一個轉換的推廣形式; Tn (t)是第一類切比雪夫多項式。 |
| 22 |  | 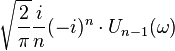 | 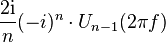 | Un (t)是第二類切比雪夫多項式。 |
[編輯]分佈
| 時域訊號 | 角頻率表示的 傅立葉轉換 | 弧頻率表示的 傅立葉轉換 | 註釋 | |
|---|---|---|---|---|
  | 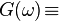  | 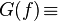 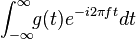 | ||
| 23 |  |  |  | δ(ω) 代表狄拉克δ函數分佈. 這個轉換展示了狄拉克δ函數的重要性:該函數是常函數的傅立葉轉換 |
| 24 |  |  |  | 轉換23的頻域對應 |
| 25 | 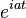 | 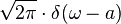 |  | 由轉換3和24得到. |
| 26 | 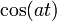 | 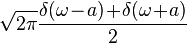 | 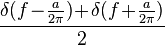 | 由轉換1和25得到,應用了尤拉公式:cos(at) = (eiat + e − iat) / 2. |
| 27 |  |  | 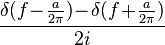 | 由轉換1和25得到 |
| 28 |  |  |  | 這裏, n 是一個自然數. δ(n)(ω) 是狄拉克δ函數分佈的n階微分。這個轉換是根據轉換7和24得到的。將此轉換與1結合使用,我們可以轉換所有多項式。 |
| 29 |  | 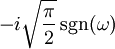 |  | 此處sgn(ω)為符號函數;注意此轉換與轉換7和24是一致的. |
| 30 | 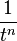 |  |  | 轉換29的推廣. |
| 31 |  | 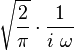 | 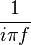 | 轉換29的頻域對應. |
| 32 |  | 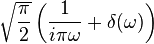 |  | 此處u(t)是單位階躍函數; 此轉換根據轉換1和31得到. |
| 33 |  | 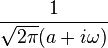 | 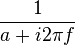 | u(t)是單位階躍函數,且 a > 0. |
| 34 |  |  | 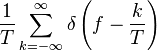 | 狄拉克梳狀函數——有助於解釋或理解從連續到離散時間的轉變. |
[編輯]二維函數
| 時域訊號 | 角頻率表示的 傅立葉轉換 | 弧頻率表示的 傅立葉轉換 | 註釋 |
|---|---|---|---|
![\mathrm{exp}\left[-\pi\left(a^2x^2+b^2y^2\right)\right]](http://upload.wikimedia.org/math/2/7/3/273382daccd673a678a1caa335f7bbaf.png) | ![\frac{1}{|ab|} \exp\left[-\pi\left(\frac{f^2_x}{a^2} + \frac{f^2_y}{b^2}\right)\right]](http://upload.wikimedia.org/math/4/8/c/48c2e8b48337e96658e758cb2d3f2c16.png) | 兩個函數都是高斯bumps, 而且可能都沒有單位體積. | |
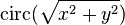 | ![\frac{J_1\left[2 \pi f_r\right]}{f_r}](http://upload.wikimedia.org/math/3/c/e/3ce4b26399cbb886736c5849d95272bb.png) | 此圓有單位半徑,如果把 circ(t) 認作階梯函數 u(1-t); Airy 分佈用 J1 (1階第一類貝索函數)表達; fr是頻率向量的量值{fx,fy}. |
[編輯]三維函數
| 時域訊號 | 角頻率表示的 傅立葉轉換 | 弧頻率表示的 傅立葉轉換 | 註釋 |
|---|---|---|---|
 | ![4 \pi \frac{\sin[2 \pi f_r] - 2 \pi f_r \cos[2 \pi f_r]}{(2 \pi f_r)^3}](http://upload.wikimedia.org/math/3/f/2/3f2824e1deb3108e6ea3b0c358873e74.png) | 此球有單位半徑;fr是頻率向量的量值{fx,fy,fz}. |
沒有留言:
張貼留言